Exponential functions are mathematical expressions where the variable is in the exponent, such as ( y = ab^x ). They model rapid growth or decay, essential in real-world applications like finance and biology. Understanding their basic form, growth vs. decay behavior, and key characteristics is fundamental for graphing and analyzing these functions.
1.1 Definition and Basic Concepts
An exponential function is defined as a mathematical expression where the variable is in the exponent, typically in the form ( y = ab^x ), where ( a ) is the initial value, ( b ) is the base, and ( x ) is the exponent. The base ( b ) determines the function’s growth or decay behavior. If ( b > 1 ), the function grows exponentially, while ( 0 < b < 1 ) results in decay. Key concepts include understanding asymptotes, domains, and ranges, which are essential for graphing and analyzing these functions effectively.
1.2 Exponential Growth vs. Decay
Exponential growth occurs when the base ( b ) of the function ( y = ab^x ) is greater than 1, causing the output to increase rapidly as ( x ) increases. Conversely, exponential decay happens when ( 0 < b < 1 ), leading to a decrease in the function's value over time. Identifying whether a function represents growth or decay is crucial for accurate graphing and real-world applications, such as modeling population growth or radioactive decay.
1.3 General Form of Exponential Functions (y = ab^x)
The general form of an exponential function is ( y = ab^x ), where ( a ) is the initial value (y-intercept) and ( b ) is the growth or decay factor. If ( b > 1 ), the function grows exponentially, while ( 0 < b < 1 ) indicates decay. This form allows for transformations, such as horizontal or vertical shifts, by adjusting ( a ) or adding constants. Understanding this structure is key for graphing and interpreting exponential behavior in various mathematical and real-world contexts.

Key Characteristics of Exponential Functions
Exponential functions have distinct characteristics, including asymptotes, intercepts, and growth or decay behavior. They exhibit exponential growth if ( b > 1 ) or decay if ( 0 < b < 1 ).
2.1 Understanding Asymptotes
An asymptote is a horizontal line that an exponential function approaches but never touches. For functions like ( y = ab^x ), the asymptote is typically ( y = 0 ). This boundary helps define the behavior of the function, whether it grows upward or decays downward. Identifying asymptotes is crucial for sketching accurate graphs and understanding the function’s limits. For example, in ( y = 2(3)^x ), the asymptote is ( y = 0 ), while transformations can shift it to ( y = c ). Always plot asymptotes first when graphing to ensure accuracy.
2.2 Identifying Intercepts
To identify intercepts for exponential functions, start with the y-intercept by setting ( x = 0 ). For example, in ( y = ab^x ), the y-intercept is ( 0, a ). Next, check for x-intercepts by setting ( y = 0 ), but note that most exponential functions do not cross the x-axis, as they approach zero asymptotically. If transformations are applied, such as vertical shifts, the x-intercept may exist. Always verify by solving algebraically and use graphing tools to confirm intercepts accurately.
2.3 Determining Growth or Decay Behavior
Determine if an exponential function exhibits growth or decay by analyzing the base ( b ). If ( b > 1 ), the function shows exponential growth, increasing rapidly. If ( 0 < b < 1 ), the function demonstrates exponential decay, decreasing toward zero. This behavior is consistent across all exponential functions, regardless of transformations. Always identify the base first to classify the function's behavior accurately, ensuring correct interpretations of growth or decay patterns in various applications and graphing scenarios.

Graphing Techniques
Mastering graphing techniques involves plotting key points, identifying asymptotes, and applying transformations. Use tables of values to sketch accurate graphs, ensuring proper scaling and axis labeling for clarity.
3.1 Plotting Points to Sketch the Graph
To sketch the graph of an exponential function, start by creating a table of values for x and corresponding y-values. Choose x-values that simplify calculations, such as integers or simple fractions. Plot these points on a coordinate plane, ensuring accurate placement. Identify the y-intercept (when x=0) and observe the behavior as x increases or decreases. Connect the points smoothly, avoiding straight lines, to form the exponential curve. Label axes clearly and include key features like asymptotes for a complete graph.
3.2 Using Transformations to Graph Functions
Transformations allow modification of the parent exponential function (y = ab^x) to sketch more complex graphs. Horizontal shifts involve adding a constant inside the exponent (y = ab^(x-h)), while vertical shifts add a constant outside (y = ab^x + k). Stretches and compressions are achieved by multiplying the base or the entire function by a factor. Identifying and applying these transformations step-by-step helps in accurately graphing exponential functions and understanding their behavior. Use transformation rules to adapt the parent function to the given equation.
3.3 Horizontal and Vertical Shifts
Horizontal shifts adjust the x-position of the graph, achieved by modifying the input variable (e.g., y = ab^(x-h)). A positive h shifts the graph right, while a negative h shifts it left. Vertical shifts alter the y-position by adding a constant to the function (e.g., y = ab^x + k). A positive k shifts the graph up, and a negative k shifts it down. These shifts do not affect the asymptote but change the graph’s position, essential for accurately sketching transformed exponential functions.
3.4 Stretch and Compression Transformations
Stretch and compression transformations modify the base or coefficient of exponential functions, altering their growth or decay rates. A vertical stretch occurs when the coefficient (a) is greater than 1, while a compression happens when 0 < a < 1. Horizontal stretches or compressions are applied by multiplying or dividing the base (b), changing the function's period. For example, y = a(b^x) shows vertical transformations, while y = (ab)^x demonstrates horizontal transformations. These changes affect the graph's steepness but not its asymptote or overall direction. Understanding these transformations is crucial for accurately graphing exponential functions with modifications.

Common Errors to Avoid
Misidentifying exponential growth versus decay is a frequent mistake, often due to confusing the base values. Incorrectly identifying asymptotes can lead to graphing errors. Misinterpreting function behavior, such as confusing horizontal and vertical shifts, is also common.
4.1 Misidentifying Growth vs. Decay
Misidentifying whether an exponential function represents growth or decay is a common error. This occurs when the base ( b ) is misunderstood. If ( b > 1 ), the function grows, while ( 0 < b < 1 ) indicates decay. Students often confuse these, especially when transformations are applied. For example, ( y = 2(3)^{-x} ) decays, not grows. Reviewing the base value and its impact on the function's behavior helps prevent such mistakes during graphing exercises.
4.2 Incorrect Asymptote Identification
Identifying the asymptote incorrectly is a frequent mistake when graphing exponential functions. For functions of the form ( y = ab^x ), the asymptote is typically ( y = 0 ). However, horizontal shifts can change this, such as in ( y = ab^{x-c} + d ), where the asymptote becomes ( y = d ). Students often overlook these transformations, assuming the asymptote remains ( y = 0 ). Carefully analyzing the function’s structure and applying transformations correctly helps avoid such errors during graphing exercises.
4.3 Mistakes in Interpreting Function Behavior
A common error is misidentifying whether an exponential function represents growth or decay. This often stems from confusing the base of the exponent. For instance, if the base (b) is greater than 1, the function exhibits growth, while values of 0 < b < 1 indicate decay. Students also frequently misinterpret transformations, such as horizontal or vertical shifts, which can alter the function's behavior. Practicing with worksheets and reviewing examples helps refine the ability to accurately interpret these functions and their growth or decay patterns.

The Worksheet: Structure and Content
The worksheet includes a variety of problems such as graphing functions, identifying asymptotes, and determining growth or decay behavior. It also contains an answer key for self-assessment.
5.1 Types of Problems Included
The worksheet includes various problem types, such as graphing exponential functions, identifying asymptotes, and determining growth or decay behavior. Students are also asked to write equations from graphs, analyze transformations, and solve real-world applications. Additionally, there are problems requiring the identification of domains, ranges, and intercepts. Multiple-choice questions and short-answer problems are included to assess understanding. The exercises are designed to cover all aspects of exponential functions, ensuring comprehensive practice and mastery.
5.2 Worksheet Layout and Instructions
The worksheet is organized into clear sections, each focusing on specific skills, such as graphing, equation analysis, and problem-solving. Instructions are provided at the top, guiding students on tools needed and problem-solving strategies. Each problem is numbered and includes space for detailed work. Graphs are accompanied by axes and grids to aid sketching. Directions emphasize accuracy, neatness, and justifying answers. Resources like rulers and tracing paper are recommended for precise graphing. The layout ensures logical progression from basic to advanced problems, promoting systematic learning and review.
5.3 Answer Key and Solutions
The worksheet includes a comprehensive answer key with detailed solutions, enabling students to verify their work and understand their mistakes. Solutions are provided for all problems, covering graphing, asymptote identification, and growth/decay analysis. Step-by-step explanations are included for complex tasks, helping students grasp concepts and improve their problem-solving skills. The answer key is typically located at the end of the document, making it easy for students to review and learn from their errors.
Using the Worksheet Effectively
To maximize learning, work through problems methodically, checking answers in the key. Focus on understanding mistakes to improve problem-solving skills and grasp exponential function concepts.
6.1 Step-by-Step Problem Solving
Begin by identifying the function type and determining if it represents growth or decay. Plot key points like (0, a) and (1, ab) to sketch the graph. Identify asymptotes and apply transformations if needed. Use the worksheet’s answer key to verify solutions and understand errors. This methodical approach ensures clarity and accuracy, helping students master graphing exponential functions effectively for tests and real-world applications.
6.2 Checking Work and Understanding Mistakes
After completing problems, compare answers with the provided key to identify errors. Review each step to pinpoint mistakes, focusing on common pitfalls like misidentifying asymptotes or misapplying transformations. Use color-coding or highlighting to track corrections. Reflect on errors to improve understanding and retention. Regularly reviewing mistakes helps build accuracy and confidence in graphing exponential functions, ensuring better performance on tests and future assignments.
6.3 Time Management and Strategy
Effective time management is crucial when working on graphing exponential functions. Start by planning your approach, prioritizing problems based on difficulty. Allocate specific time slots for sketching graphs, identifying asymptotes, and interpreting function behavior. Break complex problems into smaller, manageable steps to avoid overwhelm. Regular practice helps improve speed and accuracy. Review past mistakes to refine strategies and maintain focus during lengthy sessions. Balancing speed with precision ensures efficient problem-solving and builds confidence in tackling exponential functions effectively.
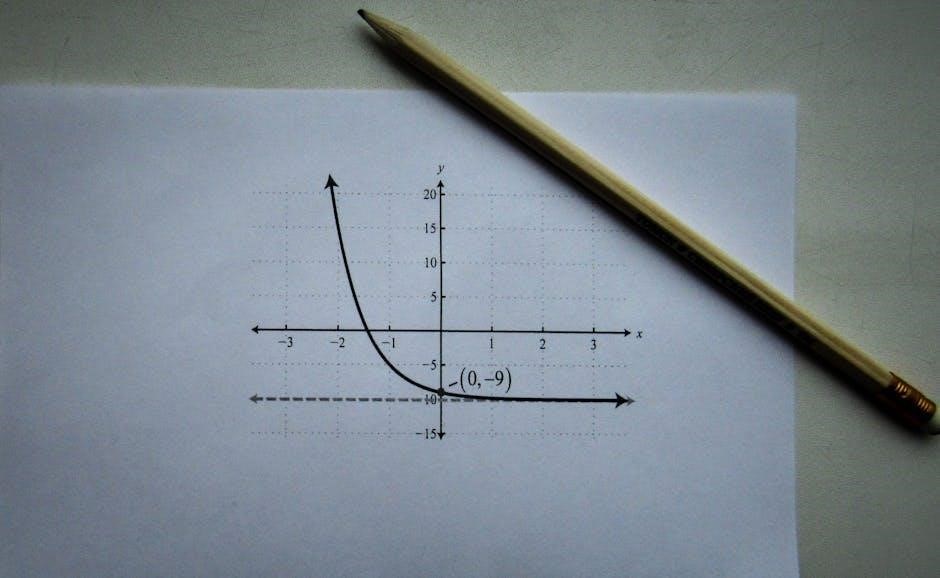
Examples and Solutions
Example: Graph ( y = 2^x ) and identify its asymptote. Solution: Plot points like (0,1) and (1,2). The asymptote is ( y = 0 ). This demonstrates exponential growth.
7.1 Example Problems with Detailed Solutions
Example 1: Graph the function ( y = 2^x ). Solution: Identify the asymptote ( y = 0 ), plot points (0,1), (1,2), and (2,4). This shows exponential growth. Example 2: Graph ( y = (1/2)^x ). Solution: Identify the asymptote ( y = 0 ), plot points (0,1), (1,0.5), and (2,0.25). This shows exponential decay. Detailed solutions include step-by-step graphing instructions and explanations of growth or decay behavior.
7.2 Graphing Exponential Functions with Transformations
Transformations modify the basic exponential function (y = ab^x). Horizontal shifts occur when x is replaced by (x ― h), while vertical shifts happen when a constant k is added; For example, y = 2^(x-3) has a horizontal shift of 3 units right. Stretches/compressions are seen when the base is multiplied by a factor. For instance, y = 3^(2x) compresses the graph horizontally. Identifying these transformations helps in sketching accurate graphs, essential for understanding function behavior.
7.3 Real-World Applications of Exponential Functions
Exponential functions model real-world phenomena like population growth, radioactive decay, and financial investments. In finance, they calculate compound interest, while in biology, they track cell division or disease spread. Understanding these functions helps predict future trends, such as estimating tumor growth rates or determining the time for an investment to double. Real-world examples make learning exponential functions engaging and relevant, connecting abstract math to practical, everyday applications.

Test Preparation and Strategies
Practice with worksheets, focus on understanding asymptotes, and allocate time wisely. Mastering key concepts ensures confidence in graphing and interpreting exponential functions during exams.
8.1 Tips for Graphing on Tests
When graphing exponential functions on tests, start by identifying whether the function represents growth or decay. Plot key points like (0, a) and (1, ab) to establish the curve’s shape. Use transformations to adjust the graph based on the function’s form. Always label asymptotes and ensure the graph does not intersect them. Double-check your work for accuracy, and use any remaining time to verify your answers. Clear labeling and organized plotting are essential for scoring well.
8.2 Understanding Asymptotes and Intercepts
Identifying asymptotes and intercepts is crucial for accurately graphing exponential functions. The horizontal asymptote, typically y=0 for exponential functions, indicates the behavior of the graph as x approaches infinity or negative infinity. Intercepts occur where the graph crosses the x-axis (y=0) or y-axis (x=0). For exponential functions, the y-intercept is always the initial value of the function when x=0. Understanding these features helps in sketching the graph correctly and interpreting the function’s behavior. Always double-check your calculations to ensure accuracy.
8.3 Multiple-Choice and Short Answer Strategies
When tackling multiple-choice questions on exponential functions, eliminate incorrect options by recalling key characteristics like asymptotes and growth/decay behavior. For short answers, clearly state the function’s form, identify asymptotes, and describe transformations. Always verify calculations and logical steps to ensure accuracy. Practice interpreting graphs and equations to strengthen understanding. Understanding the difference between growth (b > 1) and decay (0 < b < 1) is critical for selecting the right answers efficiently.

Resources and References
Recommended resources include Kuta Software for worksheets, Corbettmaths for exponential graphs guidance, and Big Ideas Math for comprehensive problem sets and solutions. These tools aid effective learning.
9.1 Recommended Textbooks and Online Resources
For mastering exponential functions, recommended textbooks include “Big Ideas Math Algebra 2” and “Algebra 1” by Kuta Software. Online resources like Corbettmaths and Khan Academy offer detailed guides and practice worksheets. Desmos and GeoGebra provide interactive graphing tools, while JMAP and Infinite Algebra 2 supply additional problem sets. These resources ensure comprehensive learning, from theoretical concepts to practical graphing skills, catering to both beginners and advanced students.
9.2 Graphing Tools and Software
Popular tools like Desmos and GeoGebra offer interactive platforms for graphing exponential functions. Kuta Software provides worksheets with answers for practice. Corbettmaths and Khan Academy supply detailed guides and step-by-step solutions. Additionally, online platforms like JMAP and educational apps such as Mathway assist with visualizing and analyzing exponential graphs. These resources enable students to explore functions dynamically, enhancing their understanding of growth, decay, and transformations.
9.3 Additional Practice Worksheets
Supplement your learning with extra practice worksheets available online. Kuta Software offers downloadable PDFs with exponential function problems, covering graphing, asymptotes, and growth/decay analysis. Corbettmaths provides detailed worksheets with solutions, while JMAP includes exponential function exercises. These resources cater to various skill levels, ensuring comprehensive practice for students. They are ideal for reinforcing concepts, preparing for exams, or exploring real-world applications of exponential functions. Regular practice with these worksheets enhances problem-solving skills and understanding of exponential behavior.

Interactive Learning Opportunities
Engage with online simulators and graphing tools to visualize exponential functions. Participate in educational games and quizzes for interactive learning. Collaborative activities enhance understanding and practical application of concepts.
10.1 Online Simulators and Graphing Tools
Utilize online simulators like Desmos and GeoGebra to explore exponential functions interactively. These tools allow real-time graphing, enabling students to visualize transformations and behavior. Features include zooming, panning, and dynamic adjustments to parameters. Kuta Software and Corbettmaths provide additional resources for practice. Such platforms facilitate deeper understanding by letting users experiment with different bases and coefficients. They are ideal for identifying asymptotes, checking homework answers, and reinforcing concepts learned in worksheets.
10.2 Educational Games and Quizzes
Educational games and quizzes enhance engagement with exponential functions. Platforms like Kahoot and Quizlet offer interactive activities that test knowledge of graphing, growth vs. decay, and asymptotes. Quizizz provides sets of questions for self-assessment, while Math Games offers puzzles that reinforce understanding. These tools complement traditional worksheets, making learning dynamic and enjoyable. They help students identify strengths and weaknesses, fostering confidence and fluency in graphing exponential functions effectively.
10.3 Collaborative Learning Activities
Collaborative learning activities foster teamwork and deepen understanding of exponential functions. Students can work in groups to solve graphing problems, share insights, and discuss common challenges. Peer teaching encourages students to explain concepts to one another, reinforcing their own knowledge. Group projects, such as creating interactive presentations or solving real-world applications, promote active learning. Additionally, collaborative problem-solving sessions allow students to exchange strategies and learn from each other’s strengths, enhancing overall mastery of graphing exponential functions.

Assessment and Feedback
Assessment and feedback are crucial for evaluating student understanding of exponential functions. Homework and quizzes provide regular checks on progress, while detailed feedback helps students refine their graphing skills and conceptual knowledge. Final exams assess comprehensive mastery, ensuring readiness for advanced topics. Consistent evaluation and constructive feedback foster continuous improvement and confidence in graphing exponential functions accurately.
11.1 Homework and Quiz Assignments
Homework and quiz assignments are essential for reinforcing concepts related to graphing exponential functions. These assignments typically include problems like graphing specific functions, identifying asymptotes, and determining whether a function represents growth or decay. Students are often asked to sketch graphs, analyze transformations, and interpret real-world applications. Quizzes may also include short-answer questions to assess understanding of key concepts. Regular assignments help students practice consistently, ensuring they master graphing techniques and can apply them accurately. Detailed feedback and answer keys are provided to improve understanding and address common mistakes.
11.2 Understanding Feedback and Revising Work
Understanding feedback and revising work are crucial steps in mastering graphing exponential functions. Feedback highlights strengths and areas for improvement, helping students refine their graphing skills. Reviewing mistakes, such as incorrect asymptote identification or mislabeling growth vs. decay, allows for targeted practice. Revising work based on feedback ensures deeper understanding and accuracy. Encouraging students to reflect on their errors fosters a growth mindset and improves problem-solving abilities. Regular revision helps build confidence and proficiency in graphing exponential functions effectively.
11.3 Preparing for Final Exams
Preparing for final exams requires consistent practice and review of graphing exponential functions. Focus on understanding key concepts like asymptotes, intercepts, and growth vs. decay behavior. Practice graphing transformations and analyzing function behavior. Review homework and quiz feedback to identify weak areas. Seek additional help if needed, and organize study materials effectively. Time management during exams is critical, so practice graphing under timed conditions. Ensure understanding of common errors to avoid them. Confidence and accuracy will improve with thorough preparation and review.
Consistent practice and review are essential for mastering graphing exponential functions. Use worksheets and resources effectively to build confidence and enhance your understanding of these concepts.
12.1 Summary of Key Concepts
Exponential functions are expressed as ( y = ab^x ), modeling growth or decay. Key concepts include identifying asymptotes, determining growth/decay behavior, and applying transformations. Graphing involves plotting points, understanding domains/ranges, and recognizing horizontal/vertical shifts. Mastery requires consistent practice, utilizing worksheets and online tools. These resources help reinforce understanding of exponential functions’ characteristics and applications, ensuring proficiency in graphing and analyzing their behavior effectively.
12.2 Encouragement for Further Practice
Consistent practice is essential for mastering exponential functions. Use worksheets and online tools to refine graphing skills and explore real-world applications. Set achievable goals, track progress, and seek feedback to improve understanding. Engage with interactive simulations and collaborative activities to deepen knowledge. Remember, practice builds confidence and proficiency, helping you excel in graphing and analyzing exponential functions effectively.



